Arc Length
Through our discussions on integration techniques, we have learned how to use integration in order to calculate the area of different regions, and even the volume of different solids. In this module, we will learn how to use integration to calculate the length of different curves.
Imagine that we have a simple, straight line that runs from the point $(x, f(x))$ to $(x+\Delta x, f(x+\Delta x))$.
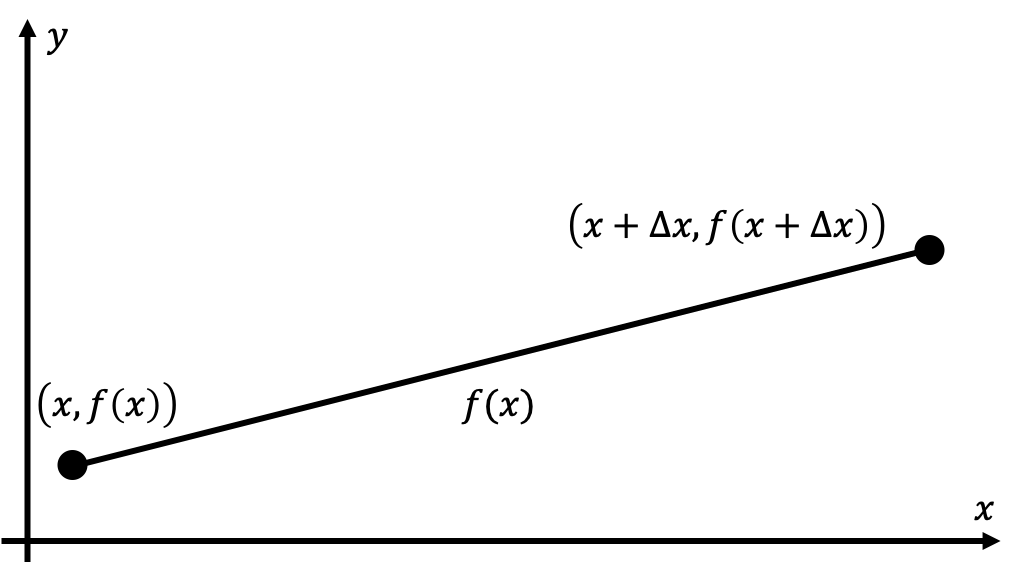
From using the distance formula from geometry, we know that the total straight-line distance between these two points $\Delta D$ is given by
\[\Delta D=\sqrt{(x+\Delta x-x)^2+(f(x+\Delta x)-f(x))^2}\]This is fairly straightforward because we are calculating the straight-line distance between two points. However, what if we instead have an arbitrarily shaped curve that we want to calculate the length of?
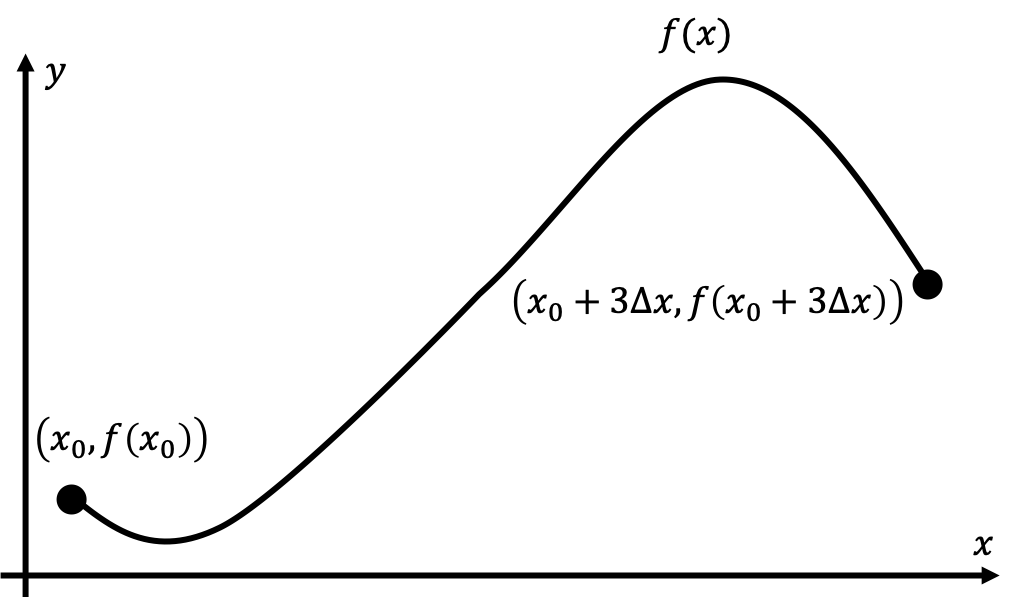
It’s a little bit more difficult now, but if we think back to our common theme behind all of integration, a potential solution would be to subdivide the entire length of the curve into very small segments, such that within each segment, the curve looks as if it was a straight line.
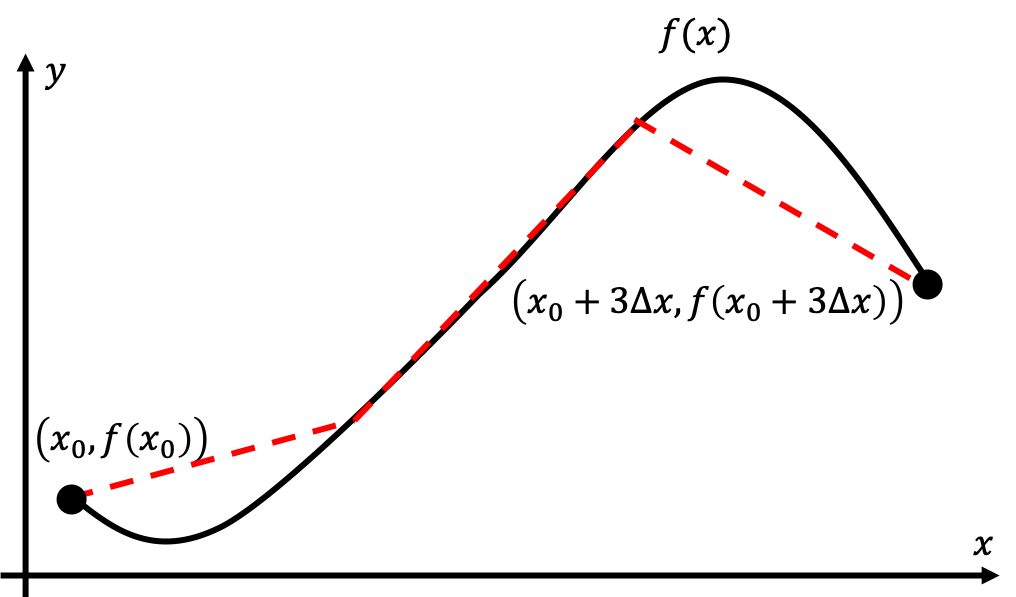
The first and third line segment approximations obviously don’t look like they approximate the length of the respective segments well, but if we take the width of each interval $\Delta x$ to be very small, such that they do look like they’re good approximations of each of the smooth curve segments, then our approximation will indeed become pretty good. In fact, our approximation will become exact as $\Delta x\rightarrow 0$. What we’ve done is essentially subdivide our complex problem into many simpler problems. For example, in the above case, we might approximate the distance $D$ between the two points $P_1$, $P_2$ as
\(D\approx\sqrt{(\Delta x)^2+(f(x_0+\Delta x)-f(x_0))^2}\) \(+\sqrt{(\Delta x)^2+(f(x_0+2\Delta x)-f(x_0+\Delta x))^2}\) \(+\sqrt{(\Delta x)^2+(f(x_0+3\Delta x)-f(x_0+2\Delta x))^2}\)
In general, for $n$ subdivisions, the formula for $D$ might look something like
\[D\approx \sum_{j=1}^n \sqrt{(\Delta x)^2+(f(x_j)-f(x_j-\Delta x))^2}\]where $x_j=x_0+j\Delta x$. Now, we’ll do some follow-up algebraic manipulation. We can factor out a factor of $\Delta x$ from the right hand side to get
\[D\approx \sum_{j=1}^n \Delta x\sqrt{1+\left(\frac{f(x_j)-f(x_j-\Delta x)}{\Delta x}\right)^2}\]What happens as $\Delta x\rightarrow 0$, such that $n\rightarrow \infty$? Firstly the expression in the square root on the right hand side simplifies to
\[D\approx \sum_{j=1}^n \Delta x\sqrt{1+\left(\left.\frac{df}{dx}\right\vert_{x=x_j}\right)^2}\]Furthermore, $\Delta x$ becomes $dx$, and the summation on the right hand side becomes an integral expression. Therefore, we can conclude that
$$D=\int_{x_i}^{x_f}dx\sqrt{1+\left(\frac{df}{dx}\right)^2}$$
Some Test Cases
First, let’s try out a couple of test cases to see if this formula that we’ve found to compute the length of different two-dimensional curves agrees with our previous formulas developed from geometry classes.
Straight Line
Imagine that we have a straight line curve of $y=mx+b$ from $x=0$ to $x=x_0$. From the distance formula from geometry, we know that the length of the curve between these two $x$-values is
\[D=\sqrt{(mx_0+b-b)^2+(x_0-0)^2}=\sqrt{m^2x_0^2+x_0^2}=x_0\sqrt{1+m^2}\]Quite separately, if we use the arc length integration formula that we derived above, we get
\[D=\int_0^{x_0}dx\sqrt{1+m^2}=\sqrt{1+m^2}\int_0^{x_0}dx=x_0\sqrt{1+m^2}\]Indeed, both of these formulas give us the same result.
Half-Circle
Now, imagine that we have a half-circle center at the origin with radius $r_0$, above the $x$-axis. From geometry, we know that the total circumference of the circle is $2\pi r_0$, meaning that the half-circle has a length of
\[D=\frac{1}{2}(2\pi r_0)=\pi r_0\]Let’s see if we can derive the same result using the arc length integration formula. Recall that the formula for a half-circle above the $x$-axis is $y=\sqrt{r_0^2-x^2}$, meaning that $\frac{dy}{dx}=\frac{-x}{\sqrt{r_0^2-x^2}}$ using the chain rule from differentiation. Therefore, using the arc length integration formula,
\[D=\int_{-r_0}^{r_0}dx\sqrt{1+\frac{x^2}{r_0^2-x^2}}=\int_{-r_0}^{r_0}dx\sqrt{\frac{r_0^2}{r_0^2-x^2}}\]Further simplifying gives
\[D=\int_{-r_0}^{r_0}dx\frac{1}{\sqrt{1-\left(\frac{x}{r_0}\right)^2}}\]Let us define the variable $u=x/r_0$ such that $r_0 du=dx$, and so
\[D=r_0\int_{-1}^1du\frac{1}{\sqrt{1-u^2}}\]We have seen this integral before in our discussion on trigonometric substitutions, and so using the result from that calculation, we have
\[D=r_0\left.\sin^{-1} x\right\vert_{-1}^1=r_0\left(\frac{\pi}{2}-\frac{-\pi}{2}\right)=\pi r_0\]Comparing this result from the geometry formula from above, we can see that indeed, we do get the expected result.
Summary
In conclusion, we have established the following formulas for calculating the arc length of an arbitrary curve $f(x)$ from the point $(x_i, y_i)$ to the point $(x_f, y_f)$:
$$D=\int_{x_i}^{x_f}dx\sqrt{1+\left(\frac{df}{dx}\right)^2}$$
Of course, we can also define an analogous equation in terms of $y$. Suppose that $g(x)=f^{-1}(x)$. Then, the same arc length can be calculated according to the formula
$$D=\int_{y_i}^{y_f}dy\sqrt{1+\left(\frac{dg}{dy}\right)^2}$$
Exercises
Problem 1
The function $f(x)=\cosh x$ is called a hyperbolic cosine function, and is defined by the equation
$$f(x)=\cosh x=\frac{e^x+e^{-x}}{2}$$
Given this information, calculate the length of the function $f(x)=\cosh x$ from $x=0$ to $x=1$.
Problem 2
Calculate the length of the function $f(x)=\ln(\cos x)$ from $x=0$ to $x=\frac{\pi}{4}$.
Problem 3
Calculate the length of the function $f(x)=x^2-\frac{1}{8}\ln x$ from $x=1$ to $x=2$.
Problem 4
This is a challenge problem.
Calculate the length of the function $f(x)=e^x$ from $x=0$ to $x=1$.