Integration Practice Problems, Part 1
The following practice problems serve to review some of main concepts of integration from the past couple of lessons, up until the $u$-substitution lesson. I encourage you to attempt the problems yourself before taking a look at the solutions.
Practice Problems
Problem 1
Which of the following statement(s) are true?
- If $f(x)$ is increasing and concave up on $[a, b]$, then the left Riemann sum for $\int_a^b f(x)dx$ is an underestimate.
- If $f(x)$ is concave up on $[a, b]$, $g(x)$ is concave down on $[a, b]$, $f(a)=g(a)$, $f(b)=g(b)$, and $f(a)<f(b)$, then the left Riemann sum for $\int_a^b f(x)dx$ is less than the corresponding left Riemann sum for $\int_a^b g(x)dx$.
- If $f(x)$ is concave down on $[a, b]$, then the midpoint Riemann sum for $\int_a^b f(x)dx$ is an overestimate.
Problem 2
For the function whose values are given in the table below, $\int_0^6 f(x) dx$ is approximated by a Riemann Sum using the value at the midpoint of each of three intervals of width $2$. What is the value of the approximation?
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| $f(x)$ | 0 | 0.25 | 0.48 | 0.68 | 0.84 | 0.95 | 1 |
Problem 3
The table below gives values of a decreasing, differentiable function $f(x)$. Approximate the value of $\int_0^8 f(x)dx$ using a trapezoidal sum with four subintervals indicated by the data in the table.
| $x$ | 0 | 1 | 5 | 6 | 8 |
| $f(x)$ | 20 | 16 | 8 | 6 | 2 |
Problem 4
If $\int_2^8 f(x) dx = -10$ and $\int_2^4 f(x)dx = 6$, then what is the value of $\int_4^8 f(x)dx$?
Problem 5
Evaluate the indefinite integral
\[\int (x+3)\sqrt{x-1}dx\]Problem 6
Evaluate the indefinite integral
\[\int \frac{dx}{e^x+1}\]Problem 7
Evaluate the indefinite integral
\[\int \frac{\ln(\ln x)}{x\ln x} dx\]Problem 8
This problem is adapted from the 2016 AP Calculus AB Exam.
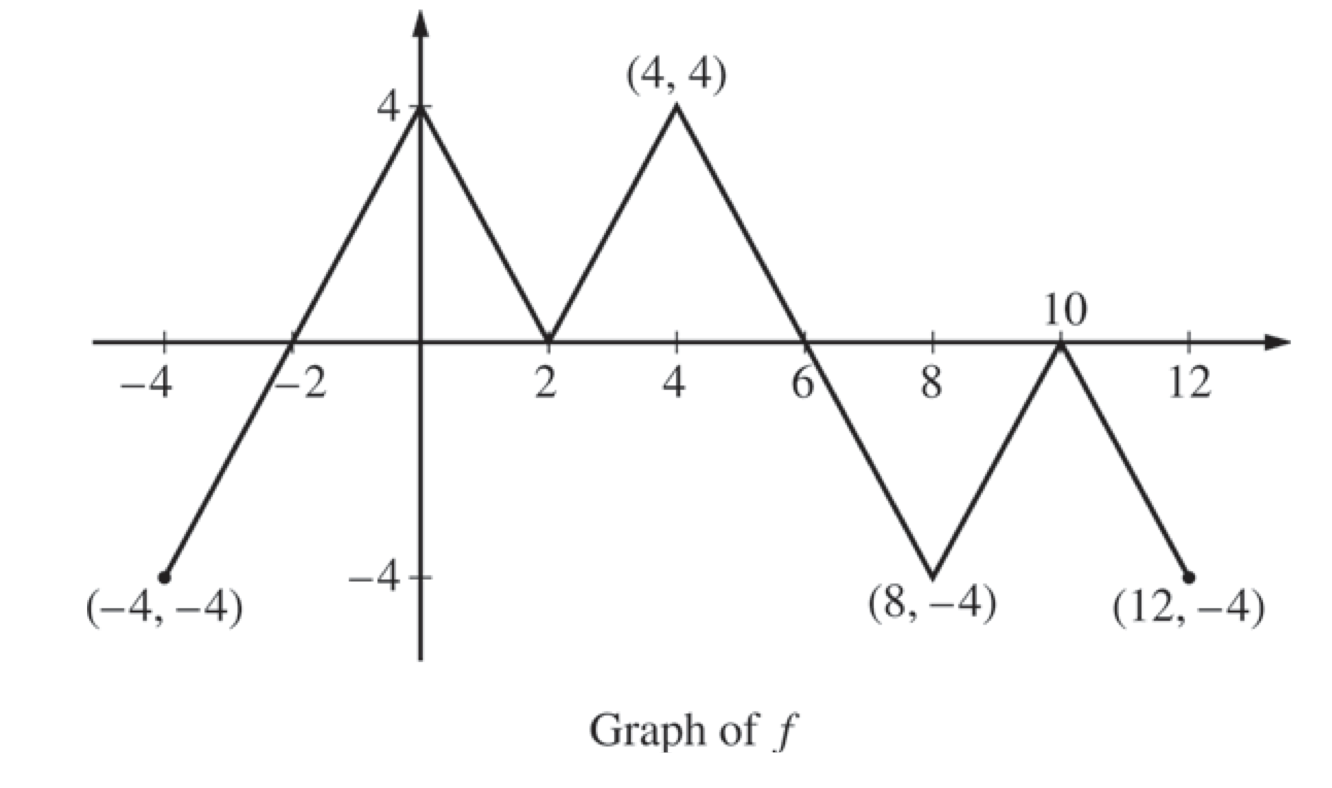
The figure above shows the graph of the piecewise-linear function $f$. For $-4\leq x\leq 12$, the function $g$ is defined by $g(x)=\int_2^x f(t)dt$.
- Does $g$ have a relative minimum, a relative maximum, or neither at $x=10$? Justify your answer.
- Does the graph of $g$ have a point of inflection at $x=4$? Justify your answer.
- Find the absolute minimum value and the absolute maximum value of $g$ on the interval $-4\leq x\leq 12$. Justify your answers.
- For $-4\leq x\leq 12$, find all intervals for which $g(x)\leq 0$.