Solids of Revolution
Over the past couple of modules, we have been focused on developing a theoretical toolkit for being able to analytically evaluate a vast range of different integrals. This involved learning techniques such as integration by parts, partial fraction decomposition, and trigonometric substitutions, among other advanced methods.
What was the point of learning all of these methods? While we have learned that computing integrals can help us, for example, compute the area underneath a curve, it turns out that another useful application of integration is to find the area of certain three-dimensional objects. Today, we’ll be learning how to use integration to find the volume of a very specific class of three-dimensional objects: solids of revolution.
What is a Solid of Revolution?
A solid of revolution can essentially be thought of as a three-dimensional object with a central axis. Because the object has a central axis, we can always form the object by taking the appropriate two-dimensional planar image and rotating it $360^{\circ}$ around the central axis. A good GIF from Wikipedia that illustrates how this works can be shown here:
Because of the unique rotational symmetry of solids of revolution, there are some different techniques that we can use to easily calculate the volume of these objects using standard integration techniques that we have been learning about.
The Basics: A Cylinder
Imagine that we wanted to perform the very simply task of calculating the volume of a cylinder with radius $r_0$ and height $h$. One way of thinking about how to approach this problem is to note that a cylinder is simply a bunch of circular disks of radius $r_0$ all stacked on top of one another to create the third dimension $h$. So, we can essentially add up all of the cylinders with base area of $\pi r_0^2$ and infinitesimal height $dx$ to create the overall cylinder. In terms of integral calculus, this looks something like this:
\[\text{volume of cylinder} = \int_0^h \pi r_0^2 dx\]A diagram of this process can look something like this:
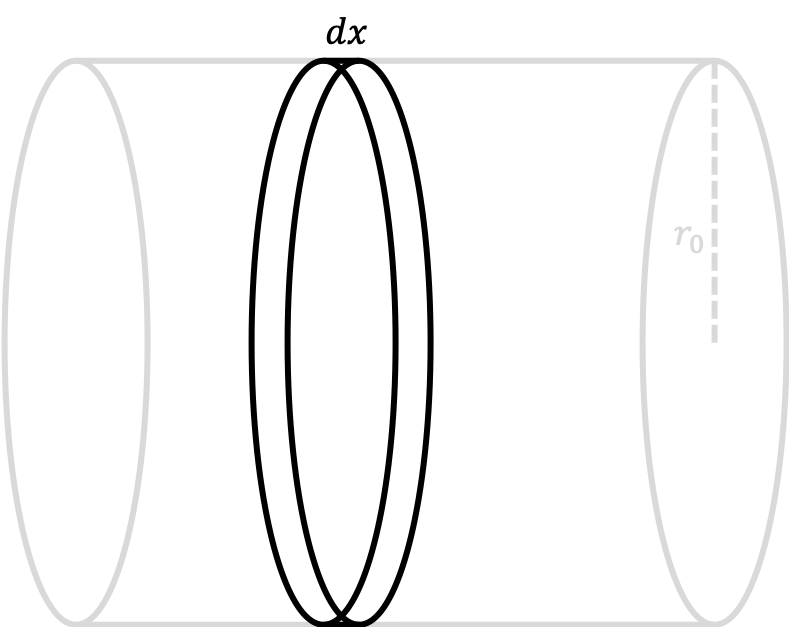
Now, let us focus on one of these little disks shown above. We can imagine the cylinder as being formed by rotating the function value $f(x)=r_0$ around the $x$-axis to create the circular disk that we see above.
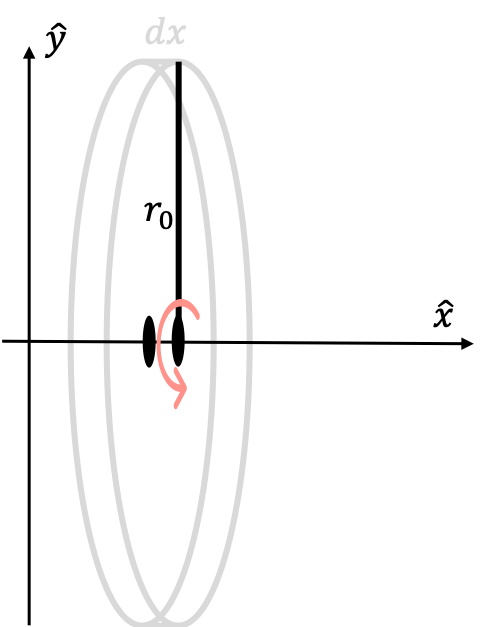
In essence, we’re able to calculate the volume of a cylinder by rotating the curve $y=f(x)=r_0$ around the $x$-axis from $x=0$ to $x=h$. We were able to do this by rotating an infinitesimally thin segment of the function $f(x)$ around the $x$-axis to form infinitesimally thin cylinders, and then add up the volumes of all of these cylinders to calculate the total volume of this particular solid of revolution. In other words, our formula for the volume $V$ is
\[V=\pi \int_0^h f(x)^2dx\]where $h$ is the height of the solid of revolution and $f(x)=r_0$ in this case. Indeed, carrying out this integration for this particular situation gives us the expected formula for the volume of a cylinder $\pi r_0^2h$ that we learned before in geometry.
A Little Harder: A Cone
Let’s imagine a little more difficult problem: evaluating the volume of a cone with the same base radius $r_0$ and height $h$. Let’s see if we can generalize our method we used to calculate the volume of the cylinder from above and use it to find the volume of the cone. In order to do this, let’s consider the graph of the function $y=\frac{r_0}{h}x$ from $x=0$ to $x=h$.
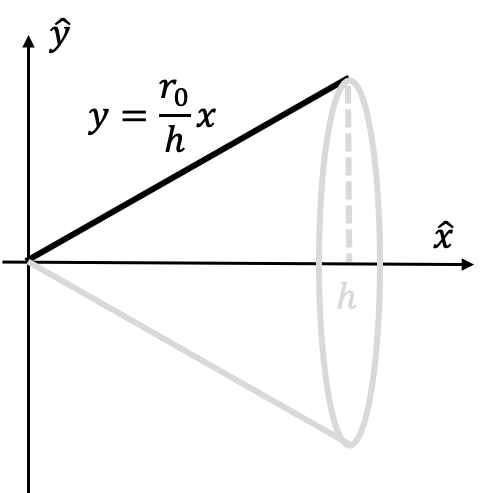
As we can see, if we rotate the described function $y=f(x)=\frac{r_0}{h}x$ about the $\hat{x}$ axis, we get exactly the geometric object and solid of revolution described: a cone with height $h$ and base radius $r_0$. Based on our work from above, we can approach this problem as subdividing the cone into many concentric cylinders of infinitesimally small heights $dx$ and radius $y=f(x)$. Using integral calculus and the formula derived above, we can sum up all of the infinitesimal volume element contributions from each of the concentric cylinders that make up the cone. Therefore, the volume $V$ of the cone is given by
\[V=\pi\int_0^h f(x)^2dx=\frac{\pi r_0^2}{h^2}\int_0^h x^2dx=\frac{\pi r_0^2}{3h^2}\left.x^3\right\vert_0^h=\frac{\pi r_0^2}{3h^2}h^3=\frac{1}{3}\pi r_0^2h\]Indeed, this is the exact formula for the volume of a cone from geometry!
A General Formula: The Washer Method
From the above two examples, we can see that we can generalize our formula for a solid of revolution formed by revolving the planar region underneath the curve $y=f(x)$ around the $x$-axis between $x=a$ and $x=b$.
The Washer Method: $V=\pi\int_a^b (f(x))^2dx$
This method is called the washer method because as per our reasoning the above two examples, we can picture this method of volume calculation as adding up the volumes of the individual solid “washer” cylinders that compose the solid of revolution.
Another Method: The Shell Method
As we discussed above, one method of approaching how to solve for the volume of an arbitrary solid of revolution is to imagine the volume as a “stack” of washers. It turns out that there is another method that relies on imagining the volume as being instead composed of concentric cylindrical shells of width $dx$. Here is a nice illustration from Wikipedia that illustrates the idea behind the shell method:
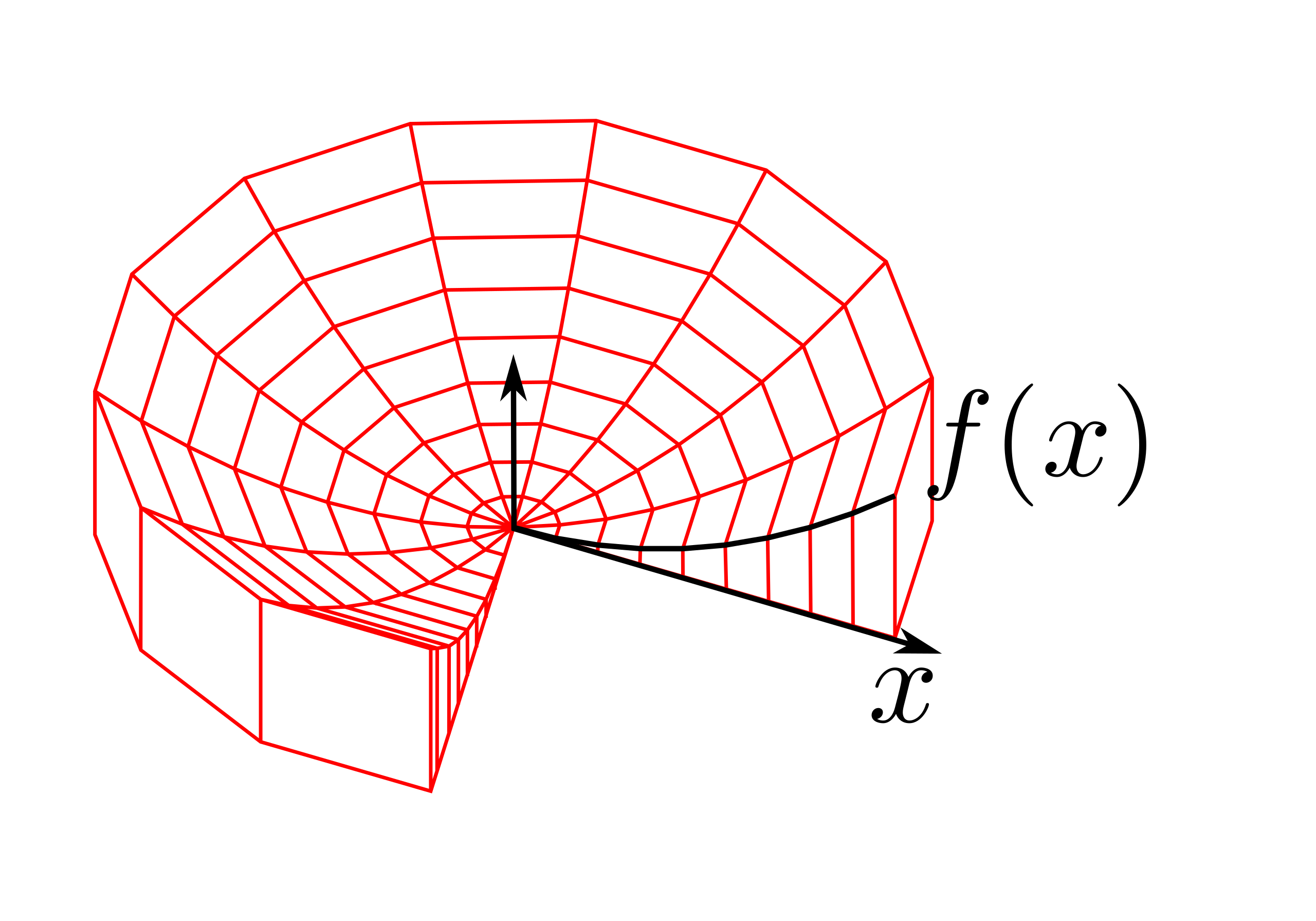
Each of the red cylindrical shells that compose the entire solid of revolution share a common axis: the $y$-axis. In this case, we can see that for a given shell at a particular value of $x$, the radius of the cylindrical shell is $x$, the thickness is the differential element $dx$, and the height of the shell is $f(x)$. Therefore, the volume of the differential element is given by
\[dV=2\pi xf(x)dx\]Note that this is only an approximation, but this approximation is good when $dx\rightarrow 0$ (which is indeed the case in our integration problems). Therefore, the total volume of a solid of revolution made by rotating the function $y=f(x)$ from $x=a$ to $x=b$ around the $y$-axis (note that it is not the $x$-axis this time) can be calculated using the shell method using the following formula:
The Shell Method: $V=2\pi\int_a^b xf(x)dx$
Summary
The volume of a solid of revolution constructed by rotating the function $y=f(x)$ from $x=a$ to $x=b$ around the $x$-axis can be found by two methods:
\[V=\pi\int_a^b(f(x))^2dx=2\pi\int_{f(a)}^{f(b)}yf^{-1}(y)dy\]The volume of a solid of revolution constructed by rotating the function $y=f(x)$ from $x=a$ to $x=b$ around the $y$-axis can be found by two methods:
\[V=\pi\int_{f(a)}^{f(b)}(f^{-1}(y))^2dy=2\pi\int_a^bxf(x)dx\]Exercises
Problem 1
Using a method similar to our derivation of the washer method above, derive a similar formula to calculate the surface area of a solid of revolution.
Problem 2
Paul’s Online Notes has an excellent set of practice problems (and associated solutions and answer explanations) that I encourage you to look over.