Writing x86 Assembly (Solutions)
The following solutions are for the problems on writing x86 84-bit assembly programs linked here. I encourage you to attempt them by yourself first before looking through the solutions.
deadbeef
Using the write() syscall, print the characters deadbeef\n to stdout without using any global static variables.
First, to print out deadbeef\n, we need to know its ASCII hexadecimal representation first. This can be determined character by character (assuming little endian convention) in this way:
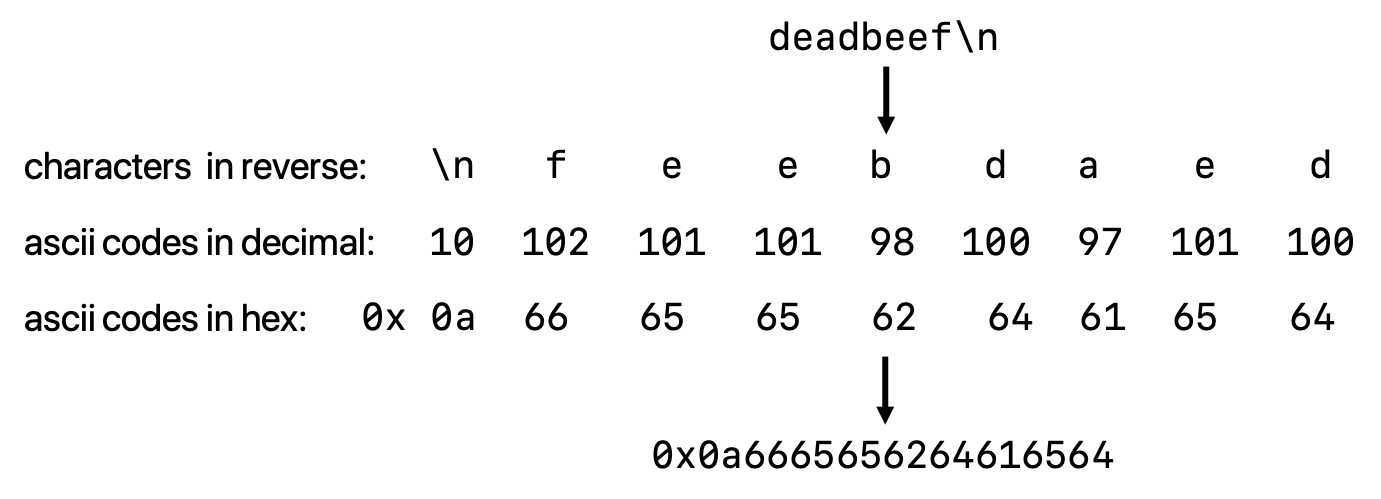
Now that we know the ASCII representation, we can implement our assembly code:
.globl main
main:
movw $0x0a, %r8w # Move \n ascii code to %r8
push %r8 # Push \n ascii code onto stack
# Move deadbeef ascii code to %r8
movq $0x6665656264616564, %r8
push %r8 # Push deadbeef ascii code onto stack
movq $0x1, %rax # System call 1 is write()
movq $0x1, %rdi # File handle 1 is stdout
movq %rsp, %rsi # Argument to write is $0x0a61 on stack
movq $9, %rdx # Number of bytes (length of string)
syscall # Invoke write() operation
pop %r8 # Restore stack state
pop %r8
retq
Notice that we have to split up the 9-byte (9-character) string into two push instructions, since a 64-bit register can only hold 8 bytes at a time.
Factorials
Write an x86 assembly program to compute the factorial of a number initially stored in %rdi.
.globl main
main:
movq $5, %rdi # Argument n (replace 5 with n)
movq $1, %r8 # Counter variable i
movq $1, %rax # Store result of n! in %rax
loop:
cmp %r8, %rdi # If n is less than the counter i...
jl exit # ...then we are done looping and exit
imulq %r8 # Multiply %rax by i
inc %r8
jmp loop
exit:
retq
Fibonacci Numbers
Write an x86 assembly program to compute the $n$th Fibonacci number, where $n$ is initially stored in %rdi.
.globl main
main:
movq $9, %rdi # Argument n (replace 9 with n)
movq $0, %r8 # Counter variable i
movq $0, %rax # Move 0th Fibonacci number to %rax
movq $1, %rbx # Move 1st Fibonacci number to %rbx
loop:
cmp %r8, %rdi # If n is less than or equal to counter i...
jle exit # ...then we are done looping and exit
movq %rbx, %rcx
addq %rax, %rcx # %rcx stores %rax + %rbx
movq %rbx, %rax
movq %rcx, %rbx
inc %r8
jmp loop
exit:
retq
Greatest Common Divisor
Using Euclid's Algorithm, calculate the greatest common divisor (GCD) of two numbers $x$ and $y$ initially stored in the registers %rdi and %rsi, respectively. Here is an implementation in Java so you can understand the algorithm:
public static int gcd(int x, int y) {
if (x == 0) { return y; }
return gcd(y % x, x);
}
Solution:
.globl main
main:
movq $9, %rdi # Argument x (replace 9 with x)
movq $6, %rsi # Argument y (replace 6 with y)
movq $0, %r8 # 0 stored in %r8
loop:
cmp %r8, %rdi # If x is 0...
je exit # ...Return y and exit
movq %rsi, %rax
cqto
idivq %rdi # Divide y by x
movq %rdi, %rsi # Set %rsi to x
movq %rdx, %rdi # set %rdi to y % x
jmp loop
exit:
movq %rsi, %rax
retq