Pulleys are going to be our first introduction to simple machines, which are contraptions that make doing work easier. In our case, a pulley typically features a wheel on an axle with a rope around it, designed to support movement and change of direction of forces. Pulleys are useful in being able to redirect the direction of forces.

Pulleys are often used in problem setups where two masses are connected by a massless string that cannot be stretched. In working with pulleys in these types of problems, the two most important things are that the existence of the pulley requires that the two masses have equal magnitudes of force (of tension from the rope) and acceleration. (We’ll see that the equal acceleration condition really only holds for one-pulley systems.) To illustrate the idea behind pulleys, we’ll show a few example problems here.

Atwood Machines

Consider the following setup:

atwood

There are only two forces acting on each of the masses: gravity and tension. Using Newton’s second law, we have

  1. $m_1g-T=m_1a$
  2. $T-m_2g=m_2a$

We have used the fact that the force of tension has equal magnitude, and also that the two masses must have the same acceleration magnitude, but in opposite directions. That is, if one mass is going downwards (which we have assumed to be $m_1$), the other mass must be going upwards. These two equations can be solved for $T, a$:

\[T=\frac{2gm_1m_2}{m_1+m_2}, \quad a=\frac{g(m_2-m_1)}{m_2+m_1}\]

The benefit of this machine is that if we want to lower mass $m_1$, $m_2$ can act as a counterweight that slows the acceleration of $m_1$, as we can see that $a<g$ from our calculations above. This can make lowering objects safer.

Multiple Pulleys

Consider the following setup:

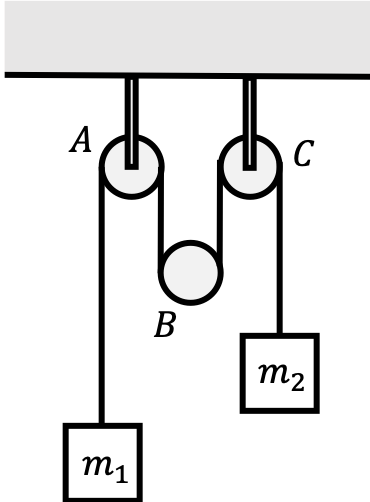
atwood

Here, we’ll assume the pulleys to be frictionless, and the ropes will also be mass. We want to fully describe the system and the acceleration of masses $m_1, m_2$, and also of Pulley $B$ with mass $m_B$. Pulleys $A$ and $C$ will be assumed to be immovable because they are held by rigid rods from the ceiling.

Equal tension everywhere throughout the rope requires the same tension force. This means that from Newton’s second law,

  1. \[T-m_1g=m_1a_1\]
  2. \[2T-m_Bg=m_Ba_B\]
  3. \[T-m_2g=m_2a_2\]

We’re assuming that $a_1, a_2, a_B$ are all in the upwards direction for convenience. These equations can be solved for $T, a_B, a_1$. This is typically because we can control $a_2$ and want to know how fast or slow the pulley and mass $m_1$ will be lowered or raised in response.

\[T=m_2(g+a_2), \quad a_B=\frac{2(m_2a_2+m_2g)-m_Bg}{m_B}, \quad a_1=\frac{m_2(g+a_2)-m_1g}{m_1}\]

Note that for multiple pulleys, we can’t necessarily equate the accelerations. In these cases, we might assume that there’s some extra rope “hidden” in the pulleys to compensate for the changes in length of the rope.

Exercises

Problem 1

Consider the following system with negligible friction and a massless rope.

atwood

Find the acceleration and force acting on both of these objects. Be sure to include the directions of the vectors as well.

Solution

Problem 2

Consider the following system with negligible friction and a massless rope.

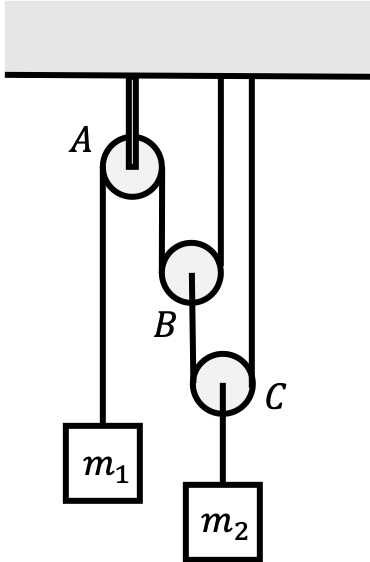
atwood

The mass of Pulley $A$ is $m_A$, the mass of Pulley $B$ is $m_B$, and the mass of Pulley $C$ is $m_C$. Find the condition on $m_2$ in terms of $m_1$ in order for the system to be in mechanical equilibrium.

Solution