Proofs

Recall the definition of the derivative that we introduced in our lesson on Introduction to Derivatives:

\[\frac{df}{dx}=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}\]

Consider the case where $f(x)=\sin x$. Plugging this into the definition of the derivative above, we find

\[\frac{d}{dx}\left[\sin x\right]=\lim_{h\rightarrow0}\frac{\sin(x+h)-\sin(x)}{h}=\lim_{h\rightarrow 0}\frac{\sin x\cos h+\cos x\sin h-\sin x}{h}\]

We expanded out $\sin(x+h)$ using the sum-of-angles rule. Using linearity of the limit definition, we can rewrite the right hand side:

\[\frac{d}{dx}\left[\sin x\right]=\cos x\lim_{h\rightarrow 0}\frac{\sin h}{h}+\sin x\lim_{h\rightarrow 0}\frac{\cos h-1}{h}\]

Using the sandwich theorem (also called the squeeze theorem), it can be shown that $\lim_{h\rightarrow 0}\frac{\sin h}{h}=1$ and $\lim_{h\rightarrow 0}\frac{\cos h -1}{h}=0$ (you will prove this in an exercise below). Plugging these results in, we find

\[\frac{d}{dx}\left[\sin x\right]=(1)\cos x+(0)\sin x=\cos x\]

This result tells us that the derivative of $\sin x$ is simply $\cos x$. Let’s see if this intuitively makes sense by plotting both of these functions together:

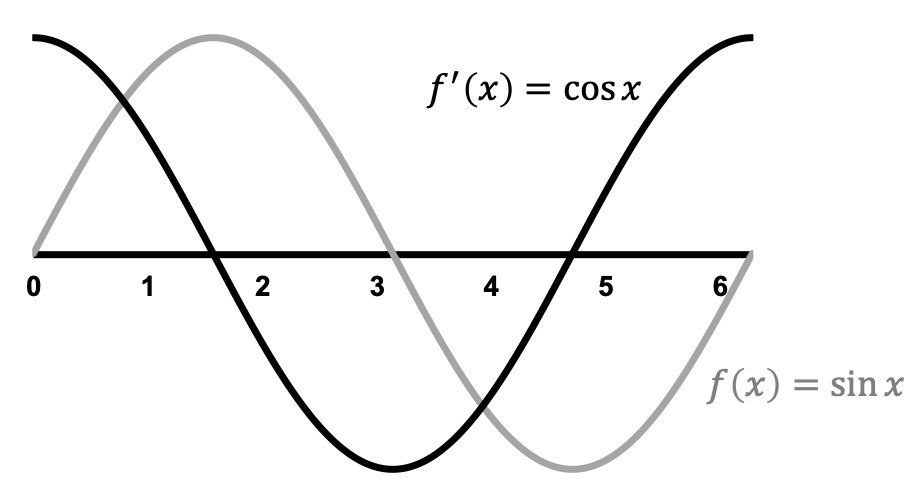
sin-derivative

At $x=0$, $\sin(x)=0$, and moreover, it is increasing very rapidly. Therefore, it makes sense that its derivative is positive ($\cos(x)=1$). At $x=\pi/2$, $\sin(x)$ achieves its maximum value, and local maxima correspond to a derivative equal to zero, which makes sense since $\cos(\pi/2)=0$. At $x=\pi$, $\sin(x)=0$, and more importantly, it is decreasingly very rapidly. Therefore, it makes sense that its derivative if negative ($\cos(x)=-1$). With these cursory checks, its clear that $\frac{d}{dx}[\sin x]=\cos x$ seems to be a fairly valid statement.

Let’s also consider the derivative of $f(x)=\cos x$, using the same definition of the derivative from above.

\[\frac{d}{dx}[\cos x]=\lim_{h\rightarrow 0}\frac{\cos(x+h)-\cos(x)}{h}=\lim_{h\rightarrow 0}\frac{\cos x\cos h-\sin x\sin h-\cos x}{h}\]

We again expanded out $\sin(x+h)$ using the sum-of-angles rule. Continuing with the same process as above for $f(x)=\sin x$,

\[\frac{d}{dx}[\cos x]=\cos x\lim_{h\rightarrow0}\frac{\cos h-1}{h}-\sin x\lim_{h\rightarrow 0}\frac{\sin h}{h}\]

Using the same special limit results from above, we have

\[\frac{d}{dx}[\cos x]=(0)\cos x-(1)\sin x=-\sin x\]

Therefore the derivative of $\cos x$ is $-\sin x$. Combining these results, we have

The Main Formulas

\[\frac{d}{dx}[\sin x]=\cos x, \quad \frac{d}{dx}[\cos x]=-\sin x\]

Using these two rules, we can derive the following as well:

  • \[\frac{d^n}{dx^n}[\sin x]=\begin{cases}(-1)^{n / 2}\sin x \text{ for even } n\\ (-1)^{(n-1)/2}\cos x\text{ for odd } n\end{cases}\]
  • \[\frac{d^n}{dx^n}[\cos x]=\begin{cases}(-1)^{n / 2}\cos x \text{ for even } n\\ (-1)^{(n+1)/2}\cos x\text{ for odd } n\end{cases}\]

Furthermore, we can also derive the following using the quotient rule:

  • \[\frac{d}{dx}[\tan x]=\frac{1}{\cos^2 x}=\sec^2 x\]
  • \[\frac{d}{dx}[\csc x]=-\cot x\csc x\]
  • \[\frac{d}{dx}[\sec x]=\tan x\sec x\]
  • \[\frac{d}{dx}[\cot x]=-\frac{1}{\sin^2 x}=-\csc^2 x\]

You will prove these statements in the exercises below.

Exercises

Problem 1

Using the squeeze theorem, prove the following limits:

  1. $\lim_{h\rightarrow 0}\frac{\sin h}{h}=1$
  2. $\lim_{h\rightarrow 0}\frac{\cos h-1}{h}=0$

Problem 2

  1. Find the second derivative of $f(x)=\sin x$. Repeat this for $g(x)=\cos x$.
  2. Find the third derivative of $f(x)=\sin x$. Repeat this for $g(x)=\cos x$.
  3. Find the fourth derivative of $f(x)=\sin x$. Repeat this for $g(x)=\cos x$.
  4. Find the fifth derivative of $f(x)=\sin x$. Repeat this for $g(x)=\cos x$.
  5. Do you notice any patterns? Do these results agree with the general result that we found above?

Problem 3

We gave derivatives of $\tan x, \csc x, \sec x, \cot x$ above. Prove these statements using the quotient rule and the derivatives of $\sin x, \cos x$ that we determined above.

Problem 4

Here, we will incorporate these trigonometric function derivatives into our standard repertoire of the chain rule, product rule, quotient rule, and other differentiation techniques. Evaluate the derivatives of the following functions:

  1. $f(x)=\frac{x^2\sin x}{x^2+1}$
  2. $f(x)=\sqrt{x}\cot x$
  3. $f(x)=\sqrt[3]{\sin \sqrt[3]{x}}$
  4. $f(x)=\cos(\pi x^2)$