Sets and Hashing
Learning Objectives: By the end of this learning module, you should understand how to...
- use the set interface and its associated implementation in Java in the appropriate contexts and usage cases.
- implement hashing has a programming feature appropriately.
- write your own set implementation.
Introduction
Imagine that you have a number of friends and wanted to tell your mom who your friends are. All of your three friends–Alice, Bob, and Charlie–are all very good friends, and so there is no particular order to them. You might tell your mom that your friends are “Alice, Bob, and Charlie,” or on a whim you might instead tell your mom that your friends are “Bob, Charlie, and Alice,” or even “Charlie, Bob, and Alice.”
The point is that there is no particular order to your friends. Imagine that you know wanted to represent your three friends as a single Java data structure. Our first instinct might be to generate an array or list, but there is no reason to necessarily maintain a particular order of your friends, which is a crucial feature of the list interface. In fact, if you decide to list your friends in something like
String[] friends = { Bob, Charlie, Alice };
Alice might even become a little upset that you listed her last and may think that you don’t value her as a friend! In this contrived example, it’s clear that there may be a better Java data structure for this application.
This is where a set comes in. A set is very similar to the mathematical concept of sets from group theory in mathematics: similar to a list, a set stores a collection of objects. However, there are a number of notable differences:
| Sets | Lists |
|---|---|
| Does not maintain a particular ordering of elements | Does maintain a particular ordering of elements |
| Duplicate elements are not allowed in the collection | Duplicate elements are allowed in the collection |
null elements are not allowed in the collection |
null elements are allowed in the collection |
| No positional access of elements | Positional access of elements |
In the last difference listed, positional access means accessing elements of either the set or the list in terms of the index. For example, list[0] would return the first element of the list list. However, set[0] is not a valid operation: you cannot access the “first” element of a set because again, there is no ordering of the set!
Now what we have an idea of what a set is, we can try to implement it in Java. It turns out that the simplest Java implementation is to use a HashSet. For example, if we wanted to create a set of integers, this might look something like
Set<Integer> mySet = new HashSet<>();
Set Operations
There are a number of things that we can do with sets. The full Java documentation for sets is here if you’re interested, but the main operations that we care about are listed here:
boolean add(E e): Adds the elementeto the set. This function does nothing ifeis already contained in the set.boolean contains(Object o): Returns whether or not the set contains the argument objecto.boolean isEmpty(): Returns whether or not the set is empty.boolean remove(Object o): Removes the objectofrom this set ifois originally present in the set.int size(): Returns the number of elements in the set.
Here are a couple example lines of Java code:
Set<Integer> mySet = new HashSet<>(); // Creates a new set
System.out.println(mySet.isEmpty()); // Prints true because nothing
// is in the set
mySet.add(6); // adds 6 to mySet
mySet.add(-1); // adds -1 to mySet
System.out.println(mySet.size()); // Prints out 2 because there are
// 2 integers in the set (6 and -1)
System.out.println(mySet.isEmpty()); // Prints false because nothing
// is in the set
mySet.remove(-1); // Removes -1 from mySet
mySet.remove(2); // Does nothing because 2 was not in the set originally
System.out.println(mySet.contains(6); // Prints true because 6 is still
// in the set
Iterating Over Sets
Because we have no positional access of set elements and the elements are not contained in a particular order, iterating over a set and going through each element is not as straightforward. Instead, we use the following alternative syntax for iterating:
Set<Integer> mySet = new HashSet<>();
for (Integer element : mySet) {
// Do something
}
The for loop is essentially saying that for each element in mySet, do something. Although we have no control over the order over which the loop will iterate over the set, it will nonetheless go through every element in the set in some order determined by the Java implementation of the set.
Introduction to Hashing
You might have noticed from above that we have already made implicit references to hashing in the small code snippets from above. For example, the Java set implementation above is a HashSet, which you might (correctly) guess is related to the concept of hashing. In this section, we’ll talk about hashing and what its purpose is.
We’ll first talk about a related thing: the hash function. A hash function is simply a function defined to map any element of type E to a finite set of integers between $0$ and $n-1$ inclusive. For example, let’s say that we are considering input elements of the type E being Integer. We might define a function badHash in the following way:
int badHash(Integer input) {
return input % n;
}
In other words, this function divides input by n and returns its remainder, which should be an integer between 0 and n-1. Another example might be a hash function for Strings, which might look like
int stringBadHash(String s) {
return s.charAt(0) % n;
}
This function takes the first character of the input string s, converts the character into a number implicitly according to ASCII convention, divides it by n and returns the remainder, which will be some number between $0$ and $n-1$ inclusive.
There are many types of hash functions that can be used to map different input variables of a particular type E to a finite range of integers. Some hash functions are better than others. In order to understand what makes a hash function “better,” we need to first understand the purpose behind hashing.
Purpose of Hashing
There are a number of different reasons why we care about hashing. Using a (good) hash function often makes it easier to compare large data sets and find elements more quickly. For example, suppose that we had a list of 1000 elements in a collection of elements and wanted to determine whether a particular element was in this collection. Without hashing, we would have to look through every single element in our collection, involving 1000 distinct comparison operations. However, if our hashing function gives relatively distinct hashed output values for each of the 1000 elements, then we might only need to compare the element we’re looking for with the elements in the collection that have the same hashed value, which can result in fewer comparisons made (and therefore a faster algorithm).
There are a couple of other purposes of hashing as well but this is the main one that we’re interested in.
Improving Hashing
We now know one potential method to classify how good or bad a potential hashing function is: we want as many unique hashing’s as possible and we want the distribution of hashing outputs to be as uniform as possible. With respect to these parameters, it turns out that the two example hashing functions we described above are very poor with respect to these parameters. We want to be able to describe better hashing functions. It turns out that some of the most widely used hash functions for integers are of the following form:
int goodHash(int K) {
return (a * K) >> (w-m);
}
This appears as a very strange function. Mathematically, what this equates to is the hash function $h_a(K)$ defined by
\[h_a(K)=\left\lfloor \frac{aK\mod 2^w}{2^{w-m}}\right\rfloor\]It’s not immediately clear why this is a good choice for a hash function, but theorists have essentially proven that this is a pretty good choice. The proof is outside the scope of our discussion. Another good example is the function
int okayHash(int K) {
return (p * K) % n;
}
where p is a prime number (common choices are 31 and 37) and n is the number of buckets, which we often restrict to powers of two for optimal performance. It turns out that a has function similar to okayHash() was used in a previous, much older version of Java, but because better functions have been developed this version is pretty outdated now. For another example, String hashing is very commonly done with the following function:
int stringGoodHash(String s) {
int hash = 0;
int power = 1;
for (int i = 0; i < s.length; i++) {
hash += (power * s.charAt(i));
power *= p;
}
return hash % n;
}
Mathematically, this function corresponds to the formula
\[h_p(s)=\sum_{i=0}^{\text{s.length}-1} s_ip^i \mod n\]where $n$ is the number of buckets (again, often chosen to be a power of 2), $s_i$ is the $i$th character of the string, and $p$ is a prime number (again, often chosen to be something like $31$ or $37$).
Note that in all of the examples from above, we often take advantage of the indivisibility of prime numbers to generate a good hash function. These hash functions are also easy to compute as well: we don’t want a hash function that’s so difficult to compute that the benefits of reduced search time for an element are zeroed out by a long and arduous computation time to even figure out what the hash output is!
Handling Hashing Collisions
Recall that the whole purpose of hashing was to make look up and accessing a particular element easier. However, what no matter how good our hashing function is, we will almost always inevitably get two or more unique elements that have the same hash function output. This phenomenon is called a collision.
There are a number of different ways to handle different collisions, but we’ll focus only one of the possible algorithms here called separate chaining. In this model, each possible “bucket” that corresponds with one of the possible array indices between $0$ and $n-1$ can hold more than one element and can be represented by a LinkedList data structure. As an example, let’s say that we have 5 buckets numbered 0 through 4, and our hash function is simply to divide by 5 and take the remainder. Suppose then that we wanted to insert the integers 11 through 16 into this hashed data structure. For the integers 11 through 15, this is pretty straight forward:
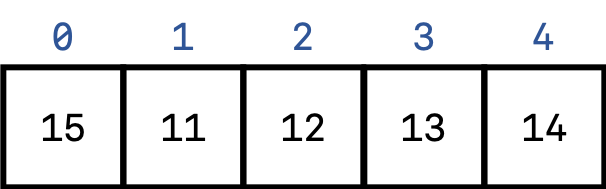
However, when we want to insert element 16 into the array, note that it should go into bucket 1 but there is already something there. Therefore, we can just insert it into a LinkedList at the array element 1, which would look something like

In this way, our array is no longer an array of integers, but an array of LinkedLists, where each LinkedList of integers represents a bucket associated with a particular array index. If we want to check if a particular element is contained in this collection, all we have to do is check with the LinkedList associated with that element’s hashed output.
There is another common way of taking care of collisions called open addressing. Problem 1 discusses this method of collision handling below.
Loading Factor
You can imagine that as we add more and more elements to our collection, we will get an increasing number/likelihood of potential collisions, which is something we obviously want to avoid. The “likelihood” of collisions can be represented by a mathematical quantity known as the loading factor $\lambda$:
\[\lambda=\frac{\text{total number of elements in the collection}}{\text{total number of buckets}}\]If the loading factor is very small, then you can imagine that we are very inefficient with our use of computer memory and resources. For example, there is no need to have 1000 buckets if there’s only one element in the collection, as that’s a complete waste of computer memory to have the 999 other unused buckets. However, if the loading fact is very large, then you can imagine that we’ll have a lot of instances of collections, and therefore in increase in search times when looking for elements in the collection. We always want to shoot for a loading factor that’s somewhere in the sweet spot: not too low but not too high. In many Java implementations of these hashed data structures, a good rule of thumb is to shoot for a loading factor of around $\lambda=0.75$.
As we add more and more elements to the collection, $\lambda$ will increase. Once $\lambda$ increases above the threshold of $\lambda=0.75$, usually what we do is double the number of buckets and re-hash all of the elements in the collection appropriately, so that the denominator of our definition for $\lambda$ effectively doubles. To see an example of this, check out the ensureLoading() function in Problem 2 below. Typically, we don’t ever worry about reducing the number of buckets.
Putting It All Together
In the sections above, we spent a lot of time describing this idea of a hashed collection of objects: elements of the same variable type would be sorted into a certain number of buckets depending on a particular hash function. It turns out that this model is a pretty good description of how Java HashSets work! HashSet have their own hash function associated with them and although this model is not perfect, it does give a pretty good idea of how these data structures work.
Hashing is a common computer programming technique that comes up over and over, and so this recurrent theme will come up again when we talk about HashTables, HashMaps, and other data structures down the road.
Exercises
Problem 1
When discussing collision handling from above, we mentioned that there is another method of handing collisions called open addressing. For this problem, answer the following questions:
- Read about the open addressing technique from GeeksforGeeks here.
- What are the benefits of open addressing compared to separate chaining? What are the downsides?
- (Optional) After completing Problem 2 below, try to modify your
MyHashSetimplementation to implement open addressing instead of separate chaining. If your performance better or worse than before?
Problem 2
Using the repl below, answer the following questions:
- Read through the code in the driver file
Main.javaand make sure you understand what the code is doing. (Comment if necessary!) - Read through the functions
hashCode()andensureLoading()inMyHashSet.javaand make sure you understand what the code is doing. (Comment if necessary!) - Implement the constructor,
add(),remove(), andcontains()functions inMyHashSet.java. - From this lesson, we learned that look-up times should be much faster when using sets instead of lists. Through running the program, you will compare the relative speeds of the
contains()functions of your implemented setMyHashSet, Java’s official set implementation, and Java’s official list implementation. How does your set implementation compare? Can you think of any ways to improve the performance of your implementation?